Optimization of inverse Snyder polyhedral projection
Abstract
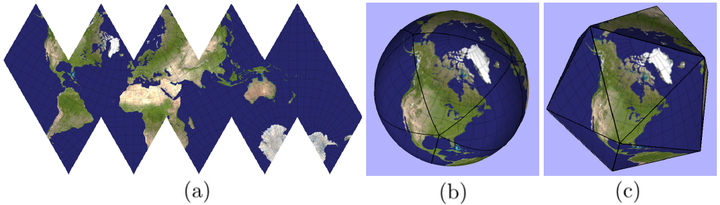
Modern techniques in area preserving projections used by cartographers and other glossarial researchers have closed forms when projecting from the sphere to the plane, as based on their initial derivations. Inversions, from the planar map to the spherical approximation of the Earth which are important for modern 3D analysis and visualizations, are slower, requiring iterative root finding approaches, or not determined at all. We introduce optimization techniques for Snyder's inverse polyhedral projection by reducing iterations, and using polynomial approximations for avoiding them entirely. Results including speed up, iteration reduction, and error analysis are provided.
Type
Publication
2011 international conference on cyberworlds (IEEE)