Multidimensional projection with radial basis function and control points selection

Abstract

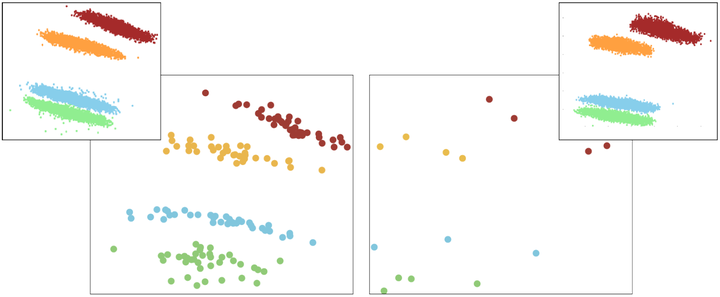
Multidimensional projection techniques provide an appealing approach for multivariate data analysis, for their ability to translate high-dimensional data into a low-dimensional representation that preserves neighborhood information. In recent years, pushed by the ever increasing data complexity in many areas, numerous advances in such techniques have been observed, primarily in terms of computational efficiency and support for interactive applications. Both these achievements were made possible due to the introduction of the concept of control points, which are used in many different multidimensional projection techniques. However, little attention has been drawn towards the process of control points selection. In this work we propose a novel multidimensional projection technique based on radial basis functions (RBF). Our method uses RBF to create a function that maps the data into a low-dimensional space …