Facing the high-dimensions: Inverse projection with radial basis functions

Abstract

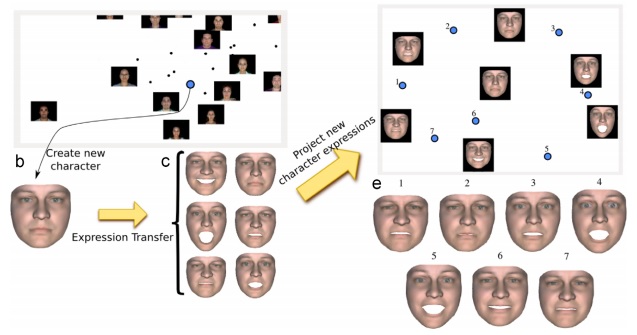
Multidimensional projection has become a standard tool for visual analysis of multidimensional data sets, as the 2D representation of multidimensional instances gives an important and informative panorama of the data. Recently, research in this topic has been steered towards methods that permit user intervention and interactivity. One of such methods is inverse projection, a recently proposed resampling mechanism that allows users to generate new multidimensional instances by creating reference 2D points in the projection space. Given an m-dimensional data set and its 2D projection, inverse projection transforms a user-defined 2D point into an m-dimensional point by means of a mapping function. In this work, we propose a novel inverse projection technique based on Radial Basis Functions interpolation. Our technique provides a smooth and global mapping from low to high dimensions, in contrast with the …