L-system description of subdivision curves

Abstract

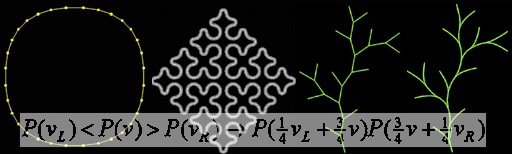
In recent years, subdivision has emerged as a major geometric modeling technique. Algorithms for generating subdivision curves are often specified in terms of iterated matrix multiplication. Each multiplication maps a globally indexed sequence of points that represents a coarser approximation of the curve onto a longer sequence that represents a finer approximation. Unfortunately, this use of matrices and indices obscure the local and stationary character of typical subdivision rules. We introduce parametric context-sensitive L-systems with affine geometry interpretation as an alternative technique for specifying and generating subdivision curves. This technique is illustrated using Chaikin, cubic B-spline, and Dyn-Levin-Gregory (4-point) subdivision schemes as examples. L-systems formalize subdivision algorithms in an intuitive, concise, index-free manner, reflecting the parallel and local character of these …