Local B-Spline Multiresolution with Example in Iris Synthesis and Volumetric Rendering

Abstract

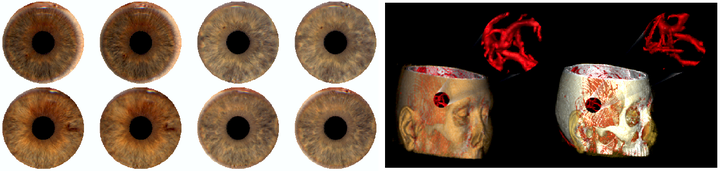
Multiresolution has been extensively used in many areas of computer science, including biometrics. We introduce local multiresolution filters for quadratic and cubic B-splines that satisfy the first and the second level of smoothness respectively. For constructing these filters, we use a reverse subdivision method. We also show how to use and extend these filters for tensor-product surfaces, and 2D/3D images. For some types of data, such as curves and surfaces, boundary interpolation is strongly desired. To maintain this condition, we introduce extraordinary filters for boundaries. For images and other cases in which interpolating the boundaries is not required or even desired, we need a particular arrangement to be able to apply regular filters. As a solution, we propose a technique based on symmetric extension. Practical issues for efficient implementation of multiresolution are discussed. Finally, we discuss some …