Multiresolution on spherical curves

Abstract

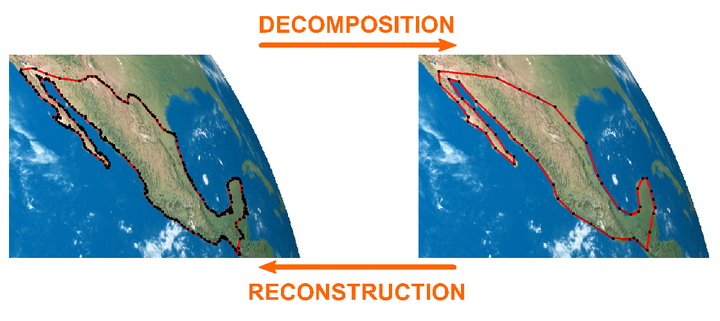
In this paper, we present an approximating multiresolution framework of arbitrary degree for curves on the surface of a sphere. Multiresolution by subdivision and reverse subdivision allows one to decrease and restore the resolution of a curve, and is typically defined by affine combinations of points in Euclidean space. While translating such combinations to spherical space is possible, ensuring perfect reconstruction of the curve remains challenging. Hence, current spherical multiresolution schemes tend to be interpolating or midpoint-interpolating, as achieving perfect reconstruction in these cases is more straightforward. We use a simple geometric construction for a non-interpolating and non-midpoint-interpolating multiresolution scheme on the sphere, which is made up of easily generalized components and based on a modified Lane–Riesenfeld algorithm.