Weather daily data approximation using point adaptive ellipsoidal neighborhood in scattered data interpolation methods

Abstract

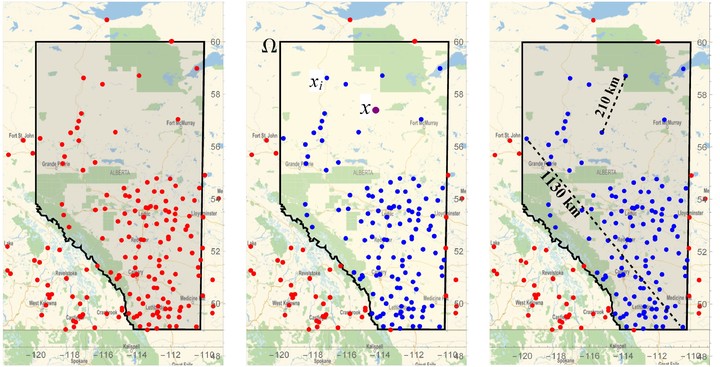
Many papers have applied the meshless method to approximate a function by using a set of scattered data. To use a meshless method, we need to predefine a positive real number as a radius of the local sphere or a positive integer as the number of interior points. This is while the effect of a fixed number as the radius of a local sphere or as the number of interior points could be different for different parts of a complex domain. This paper contains the construction of ellipsoidal neighborhoods for the meshless interpolation and approximation methods with local support functions and local behavior. By using these new neighborhoods, the trend of local data could be found easily. The advantage of this method over the current methods is the use of ellipsoidal local neighborhoods which include points with the most impact on the approximation of the function. We applied these methods to the data of the daily temperature and humidity of Alberta, Canada.